A mi modo de ver el aprendizaje automatizado, este tiene un punto de partida sencillo en la regresión lineal. Esta es la técnica más básica y simple de resolver un problema de regresión.
En este post realizaremos una regresión lineal usando un descenso de gradiente, estaremos aplicando dos de los principios en los que se sustentan muchos algoritmos complejos de ML/DL. Y es que de hecho estos dos principios son la base de las «tan de moda» redes neuronales (deep learning).
La regresión lineal y el deep learning que comparten naturaleza, en términos matemáticos una regresión lineal seria un funcional pequeñito, sencillo y lineal y las redes neuronales serian un funcional enorme y extremadamente complejo.
Lo único que varia es la complejidad, no el método.
Una pequeña introducción
En esta entrada, voy a intentar explicaros estos conceptos de la forma más simple que conozco, dibujando y con ejemplos.
Los humanos necesitamos que aquello con lo que trabajamos sea palpable, físico y visual. Desgraciadamente en DL/ML/CV esto es difícil, ya que muchas veces trabajamos con miles de dimensiones haciendo que sea complicado tener una representación física análoga. Aunque pero no imposible, existen algoritmos para la visualización de datos o reducción de la dimensionalidad.
Por eso como estamos empezando hablaremos de ejemplos sencillos, usaremos menos de 3 dimensiones (así se pueden dibujar 🙂 ).
Así que… Si habéis llegado hasta aquí y no lo habéis visto antes, os planteareis ¿Que es una regresión lineal?
La palabra regresión indica el objetivo, tratar de estimar el valor y (variable dependiente) usando el valor/valores de x (variable independiente). Matemáticamente podríamos decir que: y = f(x), donde f(x) es una función que buscamos permitiéndonos hacer dicha transformación.
La palabra lineal nos dice que la forma en la que vamos a tratar de estimar f(x) será una recta/hiperplano. Donde f(x) es una ecuación del tipo f_{A,B}(x) = Ax + B. Dos parámetros: A la pendiente, B el termino independiente.
Para explicarlo de forma simple, usaremos el siguiente ejemplo:
Tenemos una lista de personas en la que tenemos listado con su correspondiente salario y el alquiler mensual de su vivienda. Y queremos estimar el alquiler de la vivienda para futuras personas usando el salario.
| Salario /mes | Alquiler vivienda /mes |
|---|---|
| 1299€ | 1026€ |
| 1827€ | 1433€ |
| 2136€ | 1557€ |
| 1519€ | 1003€ |
| 2550€ | 1762€ |
| 2296€ | 1472€ |
| 2922€ | 1985€ |
| 1828€ | 1287€ |
| 1313€ | 993€ |
| 764€ | 598€ |
| … | … |
Difícilmente podremos deducir nada viendo la tabla (más si esta desordenada), será más fácil dibujar un mapa de puntos donde la y será alquiler y x será el salario.
Normalmente, se hace un análisis descriptivo de los datos para saber hacia donde ir.

Si nos fijamos un poco, veremos que «más o menos» podría haber una línea que relacionase ambos campos, hasta la podríamos deducir… Pero la gracia de este post no es hacerlo a mano, es aplicar ciertas técnicas para en un futuro podamos usar estas mismas en algoritmos mucho más sofisticados.
Cuantificar lo que me equivoco
Supongamos que tenemos una mínima idea de que valores podrían tener A y B. ¿Como podríamos evaluar lo bien que lo hacemos? Midiendo el error, deberíamos definir una función de error (conocida tambien como loss) que nos indique como de equivocados estamos al predecir el alquiler, es decir: Nos dirá en términos cuantitativos cómo de equivocados estamos. Existen muchos casos de problemas que no se han conseguido resolver satisfactoriamente por usar una función de error inadecuada.
En este post usaremos la MSE (Mean Square Error) aunque existen muchas más. En este caso, formula del MSE es la siguiente:
J = MSE = \frac{1}{2N} \sum_{i}^{N} {e^2}
para nosotros e = f_{A,B}(x) - y, es la estimación del alquiler (predicción) menos el alquiler real (label). Elevamos el error al cuadrado por aspectos técnicos. Se añade un \frac{1}{2} que en el futuro tendrá utilidad (no os haré spoiler) y N que es el numero de muestras (sino la magnitud de la función de error dependería del número de muestras).
Si dibujamos el error (J) por todos los valores de A y B con respecto la función: f=1x + 5, nos encontraríamos con un dibujo similar al siguiente (es solo una representación):
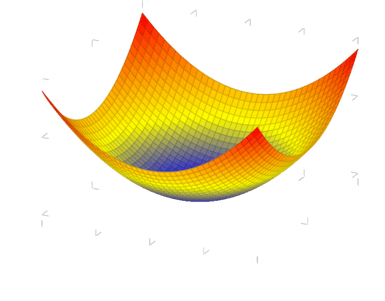
Como podemos ver, hace como una especie de cuenco, esto es porque la función de error es convexa con un mínimo global en A=1 y B=5. Esté punto es el que nuestra f_{A, B} se parece más a f = 1x + 5.
A nosotros nos interesa los parámetros A y B que menos error tienen, pero no podemos probarlos todos, así que: ¿Porque no «surfeamos» por la esta superficie para llegar al mínimo error?
Surfeando la función de error
Surfear la función de error es lo que se conoce como descenso de gradiente, básicamente lo que se hace es fijar un punto donde se empieza a surfear (normalmente aleatorio) y a partir de allí se intenta ir hacia abajo (donde se encuentra el mínimo).
![]()
De modo que en el descenso de gradiente características:
- Estado actual.
- La dirección hacia el mínimo desde el estado actual (sentido opuesto a la derivada).
¿Que implicaciones tiene esto? Que será un método iterativo. Los métodos numéricos a diferencia de los métodos de resolución exacta a cada iteración que hacen, se aproximan a la solución optima.
Esto sucede porque muchas veces es imposible encontrar un método exacto o la solución es demasiado compleja y una solución aproximada se considera suficientemente buena.
Así es como funciona:
- Miraremos hacia donde tenemos que ir.
- Conociendo la dirección actualizaremos el estado actual a una posición más cercana al mínimo.
- Realizaremos estos pasos hasta que:
- Lleguemos a un error que consideremos mínimo.
- Converja, diferencia entre estado actual y anterior sean muy similares.
- Nos cansemos, máximo de iteraciones.
Be diferentiable my friend
Antes hemos dicho que una premisa esencial es que fuese diferenciable. ¿Recordáis las aburridas clases de la ESO donde nos explicaban las poco útiles derivadas? Pues estáis muy equivocados al creer que son poco útiles. Prácticamente todos los algoritmos de aprendizaje se basan en ellas.
Pero no te asustes, una derivada lo único que hace es calcular la diferencia entre dos puntos de una función en un intervalo muy muy pequeño. De modo que la derivada indica la tendencia en un punto concreto, es decir la dirección que seguimos. Si lo miramos en sentido opuesto, es justamente lo que necesitamos para descender hacia el mínimo

Para derivar lo ideal es usar una tabla de derivadas, si teneis que deducir cada una de ellas con la ecuacion anterior probablemente tardareis un buen rato.
Pero eso no es todo, existe una regla que usaremos en este mismo articulo que es la regla de la cadena.
Esta permite construir una derivada a partir de derivadas de funciones compuestas. Es extremadamente fácil de usar y muy útil, te va a permitir derivar trozo a trozo una función que inicialmente parece muy complicada.
Está indica que:
\frac{\partial a}{\partial z} = \frac{\partial a}{\partial b} \frac{\partial b}{\partial c} \frac{\partial d}{\partial e} ....\frac{\partial x}{\partial z}
Ejemplo:
f(x) = g(x) + 3
g(x) = x^2 + x
\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g} \frac{\partial g}{\partial x} = (1)(2x + 1)
Cuando una función esta dentro de otra, la regla de la cadena permite obtener la derivada de cada profundidad en términos de la función global.
Paso final
Ya tenemos el background que necesitamos, solamente toca aplicarlo para resolver el problema.
Recordamos que nuestra función de error era la siguiente:
J = \frac{1}{2N} \sum_{i}^{N} {(f_{A,B}(x) - y)^2}
En la terminología de machine learning también la podéis encontrar como Energy.
En sí, la función de error solo nos permite saber el error para un caso concreto de A y B. Lo interesante es que su derivada respecto A (\frac{\partial J}{\partial A}) y respecto B (\frac{\partial J}{\partial B}) nos pueden guiar hacia el mínimo, porque es donde el error será lo mas pequeño posible.
\frac{\partial J}{\partial A} = \frac{\partial J}{\partial f_{A,B}} \frac{\partial f_{A,B}}{\partial A}
\frac{\partial J}{\partial B} = \frac{\partial J}{\partial f_{A,B}} \frac{\partial f_{A,B}}{\partial B}
Las partes a calcular son:
\frac{\partial J}{\partial f_{A,B}(x)} = 2 \frac{1}{2N} \sum_{i}^{N} {(f_{A,B}(x) - y)}
\frac{\partial f_{A,B}}{\partial A} = x
\frac{\partial f_{A,B}}{\partial B} = 1
El resultado es:
\frac{\partial J}{\partial A} =\frac{1}{N}\left(\sum_{i}^{N} {(f_{A,B}(x) - y)} x \right )
\frac{\partial J}{\partial B} =\frac{1}{N}\left(\sum_{i}^{N} {(f_{A,B}(x) - y )} 1 \right )
donde hemos aplicado la regla de la cadena.
Lo que vamos a hacer ahora será conectar la evolución de A y B respecto al tiempo, al error respecto el estado actual. Esto se hace de la siguiente forma.
\frac{\partial A}{\partial t} = - \frac{\partial J}{\partial A}
\frac{\partial B}{\partial t} = - \frac{\partial J}{\partial B}
Igualando las derivadas estamos diciendo que A en el tiempo progresará en sentido contrario a como progresa el error en ese estado de A (y lo mismo para B).
Como no podemos trabajar en tiempo continuo, sino en intervalos, debemos discretizar \frac{\partial A}{\partial t} y \frac{\partial B}{\partial t}.
\frac{\partial A}{\partial t} = \frac{ A_{t} - A}{t} = - \frac{\partial J}{\partial A}
\frac{\partial B}{\partial t} = \frac{ B_{t} - B}{t} = - \frac{\partial J}{\partial B}
A y B serán los estados actuales y A_{t} y B_{t} los futuros, solo debemos aislarlos.
A_{t} = A - t \frac{\partial J}{\partial A} = A - t \frac{1}{N}\left(\sum_{i}^{N} {(f_{A,B}(x) - y)} x \right )
B_{t} = B - t \frac{\partial J}{\partial B} = B - t \frac{1}{N}\left(\sum_{i}^{N} {(f_{A,B}(x) - y)} 1 \right )
Si suponemos que A y B son un vector w lo podríamos escribir de la siguiente forma:
\vec{W}<em>{t+1} =\vec{W}</em>{t} - t \ \frac{1}{N}\left(\sum_{i}^{N} {(f_{\vec{W}}(x) - y)} \begin{bmatrix}
x
\
1
\end{bmatrix} \right)
f_{W}(x) = W^T \begin{bmatrix}
x
\
1
\end{bmatrix}
El parámetro t es lo que comúnmente se conoce como learning rate, esté indica la velocidad de descenso. Esté es muy importante, porque si es muy pequeño tardarás muchísimo (porque el avance por iteración será muy pequeño), pero si es muy grande puede que nunca llegues a la mejor solución.
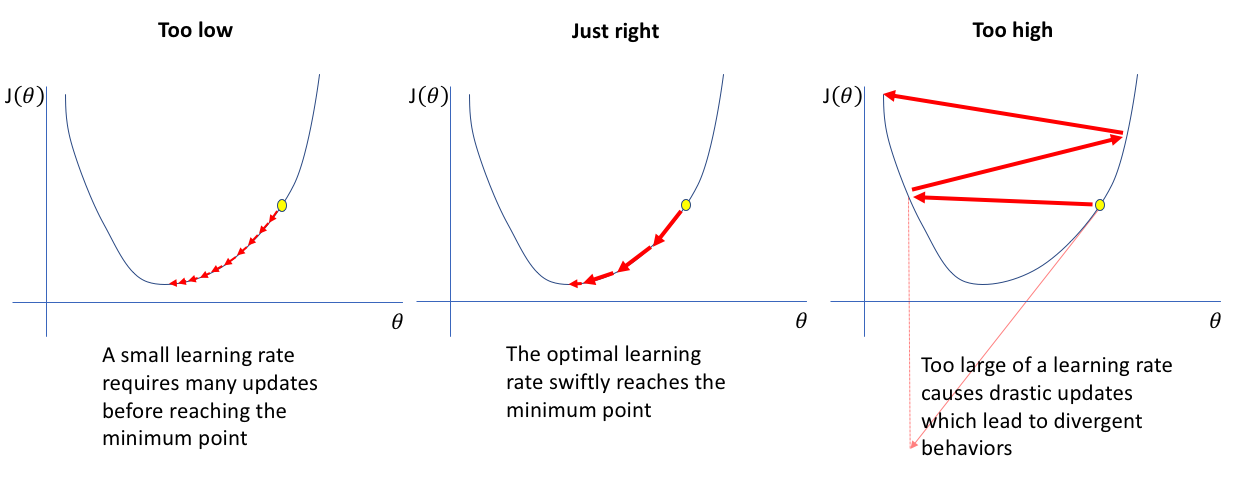
Fuente original: https://www.jeremyjordan.me/nn-learning-rate/
Código:
¡Una vez entendido, vamos a programarlo!

¡Y eso es todo! Aunque no lo creéis, conocer bien esta técnica aporta muchísima solidez en algoritmos más complejos porque muchas veces la complejidad reside en añadir capas y capas, pero el background sigue siendo el mismo.
Existen otras formas de estimar la regresión lineal que os explicaré en próximos posts.




